MLv¶
MLv is the Richter (1935) magnitude measured on the vertical component.
Description¶
Amplitude¶
The MLv amplitude calculation is very similar to the original ML, except that the amplitude is measured on the vertical component.
Station Magnitude¶
The individual station MLv is calculated up to the epicentral distance maxDistanceKm using the following formula:
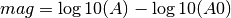
A is the MLv Wood-Anderson amplitude in millimeters. The second term is the empirical calibration function, which in turn is a function of the epicentral distance (see Richter, 1935).
The logA0 configuration string consists of an arbitrary number of distance-value pairs separated by semicolons. The distance is in km and the value corresponds to the log10(A0) term above.
Within each interval the values are computed by linear interpolation. E.g. for the above default specification, at a distance of 100 km the logA0 value would be ((-4.5)-(-2.8))*(100-60)/(400-60)-2.8 = -3.0 – in other words, at 100 km distance the magnitude would be
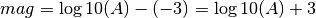
which is according to the original Richter (1935) formula if the amplitude is measured in millimeters.
- Amplitude unit in SeisComP3: millimeter (mm)
- Time window: 150 s by scautopick or distance dependent
- Default distance range: 0 - 8 deg
- Depth range: no limitation
Configuration¶
Several distance-value pairs can be configured for different ranges of epicentral distance. The calibration function and maximum distance can be configured globally, per network or per station using the configuration variables, e.g.
Set the configuration and calibration parameters in the global bindings. By deault MLv is computed by scautopick and is visible in the GUI.
