ML

ML is the Richter (1935) magnitude.

Description

Amplitude

The ML amplitude calculation is similar to the original ML. Waveforms from both horizontal components are time-windowed and restituted to the Wood-Anderson seismograph. Within the time window the amplitudes are measured on both horizontal components and combined. The methods for measuring and combining amplitudes are configurable in the global bindings.

Station Magnitude

The individual station ML is calculated using the following formula:

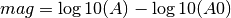
mag = \log10(A) - \log10(A0)

A is the measured ML Wood-Anderson amplitude in millimeters. The second term is the empirical calibration function, which in turn is a function of the epicentral distance (see Richter, 1935). This calibration function can be configured globally or per station using the config variable module.trunk.global.ML.logA0, e.g.

module.trunk.global.ML.logA0 = “0 -1.3;60 -2.8;400 -4.5;1000 -5.85”

The logA0 configuration string consists of an arbitrary number of distance-value pairs separated by semicolons. The distance is in km and the value corresponds to the log10(A0) term above.

Within each interval the values are computed by linear interpolation. E.g. for the above default specification, at a distance of 100 km the logA0 value would be ((-4.5)-(-2.8))*(100-60)/(400-60)-2.8 = -3.0 – in other words, at 100 km distance the magnitude would be

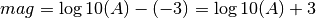
mag = \log10(A) - (-3) = \log10(A) + 3

which is according to the original Richter (1935) formula if the amplitude is measured in millimeters.

Several distance-value pairs can be configured for different ranges of epicenter distance.

  • Amplitude unit in SeisComP3: millimeter (mm)
  • Time window: 150 s by scautopick or distance dependent
  • Default distance range: 0 - 8 deg
  • Depth range: 0 - 80 km

Configuration

Set the configuration and calibration parameters in the global bindings. Add ML to the list of computed amplitudes and magnitudes in the configuration of scamp and scmag and in scesv for visibility.